Understanding R Squared: A Comprehensive Guide In 2024

Introduction to R Squared

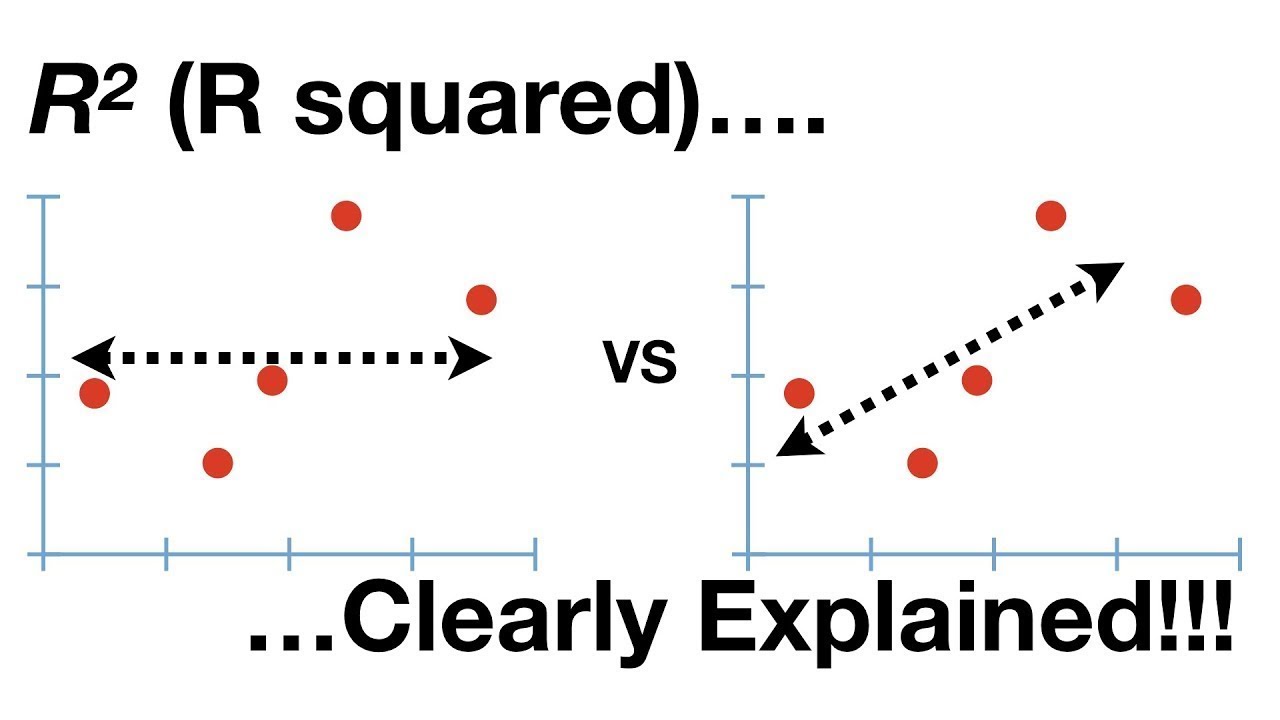
R squared, often symbolized as R², is a statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable or variables in a regression model. In simpler terms, it indicates how well data fits a statistical model. As we delve into 2024, understanding such statistical concepts becomes crucial for data enthusiasts, analysts, and anyone involved in data-driven decision-making. R squared is a fundamental concept in statistics and is widely used in various fields such as finance, economics, biology, and social sciences. This article aims to break down the complexities surrounding R squared in a relaxed and understandable manner, ensuring that even those with minimal statistical background can grasp its essence.

The Significance of R Squared in Data Analysis

In data analysis, R squared serves as a key indicator of the effectiveness of a model. It tells us how much of the variance in the dependent variable can be predicted from the independent variable(s). An R squared value of 0 indicates that the model explains none of the variability of the response data around its mean, while a value of 1 indicates that the model explains all the variability of the response data around its mean. This makes R squared a powerful tool in assessing the strength of a model. In 2024, as data becomes more pivotal in decision-making, understanding the significance of R squared helps analysts and businesses ensure their models are robust and reliable.

Calculating R Squared

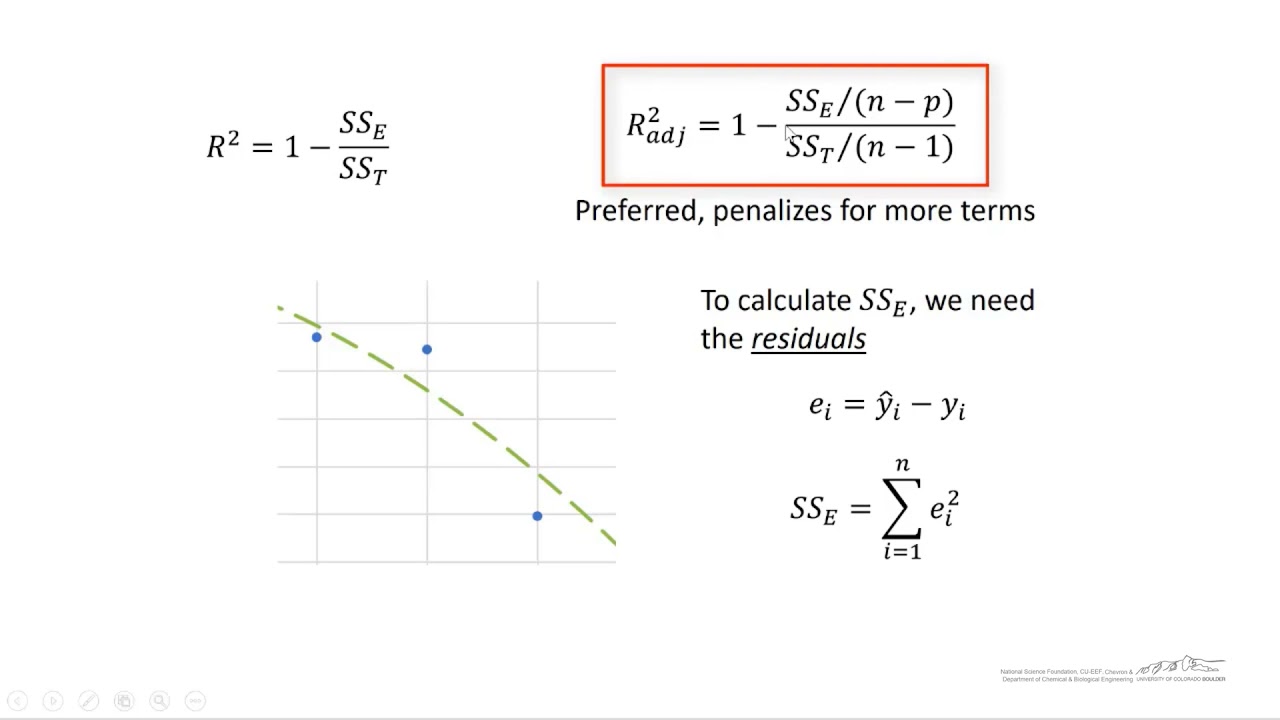
The calculation of R squared involves a few steps. First, you need the sum of squares of residuals (SSR), which is the sum of the squared differences between the observed values and the values predicted by the model. Second, you need the total sum of squares (TSS), which is the sum of the squared differences between the observed values and the mean of the observed values. R squared is calculated by subtracting the SSR from the TSS, and then dividing the result by the TSS. This formula gives a value between 0 and 1, which indicates the goodness of fit of the model. Although the calculation might seem daunting at first, it becomes straightforward with practice and the use of statistical software tools.

Interpreting R Squared

Understanding and interpreting R squared is crucial for making informed decisions based on statistical models. A high R squared value, close to 1, indicates that a large proportion of the variance in the dependent variable is predictable from the independent variable(s). However, it's important to note that a high R squared does not imply causation. It merely suggests a strong correlation. Conversely, a low R squared value indicates that the model does not explain much of the variability in the data, which could mean that the model is not suitable for the data, or that there are other influencing variables not included in the model. In 2024, as we continue to rely on data for decision-making, accurately interpreting R squared will help avoid misleading conclusions.

Limitations of R Squared

While R squared is a useful statistic, it has its limitations. One of the main criticisms is that it always increases as more predictors are added to the model, regardless of whether the predictors are meaningful. This can lead to overfitting, where the model becomes too complex and describes the random error in the data rather than the actual relationships. Another limitation is that R squared does not indicate whether a regression model is adequate, nor does it provide information on the bias of the estimates. In the context of 2024, where data models are becoming increasingly complex, it's essential to be aware of these limitations and use R squared in conjunction with other metrics, such as adjusted R squared and p-values, to assess model fit.

R Squared vs. Adjusted R Squared

Adjusted R squared is a modified version of R squared that adjusts for the number of predictors in the model. Unlike R squared, which can be artificially high when unnecessary predictors are included, adjusted R squared increases only if the new predictor improves the model more than would be expected by chance. In other words, it penalizes the addition of variables that do not improve the model. In 2024, with the growing complexity of datasets and the need for accurate models, using adjusted R squared provides a more reliable measure of model fit, especially when comparing models with different numbers of predictors.

Practical Applications of R Squared

R squared is widely used in various real-world applications. In finance, it helps in assessing the performance of investment portfolios and predicting stock prices. In marketing, businesses use R squared to understand consumer behavior and optimize advertising strategies. In environmental science, it assists in modeling climate change impacts and predicting weather patterns. As we progress through 2024, the application of R squared continues to expand, particularly with the advent of machine learning and artificial intelligence, where it helps in model evaluation and selection. Understanding its practical applications allows businesses and researchers to make data-driven decisions that are backed by statistical evidence.

Common Misconceptions about R Squared

There are several misconceptions about R squared that can lead to misinterpretation of results. One common misconception is that a high R squared indicates a good model. While a high R squared suggests a good fit, it does not guarantee that the model is appropriate. Another misconception is that R squared can show the causal relationship between variables, which is not true. R squared only measures correlation, not causation. Additionally, some believe that a low R squared is always bad, but in some cases, like exploratory research, a low R squared might be acceptable. In 2024, with the increasing reliance on data, it's crucial to address these misconceptions to ensure accurate interpretation and application of R squared.

How to Improve R Squared in Your Models

Improving R squared involves enhancing the model's ability to predict the dependent variable. One way to do this is by including additional relevant predictors that capture the variability in the data. However, care must be taken to avoid overfitting by only adding predictors that have theoretical justification and statistical significance. Another approach is transforming variables to better capture relationships, such as using logarithmic or polynomial transformations. Additionally, incorporating interaction terms can help model the combined effect of variables. As we navigate 2024, improving R squared involves a balance between model complexity and interpretability, ensuring that the model remains robust and reliable.

Conclusion: Embracing R Squared in 2024

R squared remains a cornerstone in the field of statistics and data analysis. As we advance into 2024, its relevance continues to grow, particularly in an era where data drives decision-making across industries. Understanding R squared, its calculation, interpretation, and limitations, equips analysts, researchers, and businesses with the knowledge to build robust predictive models. While R squared is a valuable metric, it should be used alongside other statistics to provide a comprehensive view of model performance. By embracing R squared and leveraging its insights, we can unlock the potential of data to inform strategies, optimize processes, and drive innovation in the years to come.